Estimating a PEM survival model with Gamma baseline hazard¶
In [ ]:
%load_ext autoreload
%autoreload 2
%matplotlib inline
import random
random.seed(1100038344)
import survivalstan
import numpy as np
import pandas as pd
from stancache import stancache
from matplotlib import pyplot as plt
In [2]:
print(survivalstan.models.pem_survival_model_gamma)
/* Variable naming:
// dimensions
N = total number of observations (length of data)
S = number of sample ids
T = max timepoint (number of timepoint ids)
M = number of covariates
// data
s = sample id for each obs
t = timepoint id for each obs
event = integer indicating if there was an event at time t for sample s
x = matrix of real-valued covariates at time t for sample n [N, X]
obs_t = observed end time for interval for timepoint for that obs
*/
// Jacqueline Buros Novik <jackinovik@gmail.com>
data {
int<lower=1> N;
int<lower=1> S;
int<lower=1> T;
int<lower=0> M;
int<lower=1, upper=N> s[N]; // sample id
int<lower=1, upper=T> t[N]; // timepoint id
int<lower=0, upper=1> event[N]; // 1: event, 0:censor
matrix[N, M] x; // explanatory vars
real<lower=0> obs_t[N]; // observed end time for each obs
real<lower=0> t_dur[T];
real<lower=0> t_obs[T];
}
transformed data {
real c_unit;
real r_unit;
int n_trans[S, T];
// scale for baseline hazard params (fixed)
c_unit = 0.001;
r_unit = 0.1;
// n_trans used to map each sample*timepoint to n (used in gen quantities)
// map each patient/timepoint combination to n values
for (n in 1:N) {
n_trans[s[n], t[n]] = n;
}
// fill in missing values with n for max t for that patient
// ie assume "last observed" state applies forward (may be problematic for TVC)
// this allows us to predict failure times >= observed survival times
for (samp in 1:S) {
int last_value;
last_value = 0;
for (tp in 1:T) {
// manual says ints are initialized to neg values
// so <=0 is a shorthand for "unassigned"
if (n_trans[samp, tp] <= 0 && last_value != 0) {
n_trans[samp, tp] = last_value;
} else {
last_value = n_trans[samp, tp];
}
}
}
}
parameters {
vector<lower=0>[T] baseline; // unstructured baseline hazard for each timepoint t
vector[M] beta; // beta for each covariate
real<lower=0> c_raw;
real<lower=0> r_raw;
}
transformed parameters {
vector[N] log_hazard;
vector[T] log_baseline;
real<lower=0> c;
real<lower=0> r;
log_baseline = log(baseline);
r = r_unit*r_raw;
c = c_unit*c_raw;
for (n in 1:N) {
log_hazard[n] = x[n,]*beta + log_baseline[t[n]];
}
}
model {
for (i in 1:T) {
baseline[i] ~ gamma(r * t_dur[i] * c, c);
}
beta ~ cauchy(0, 2);
event ~ poisson_log(log_hazard);
c_raw ~ normal(0, 1);
r_raw ~ normal(0, 1);
}
generated quantities {
real log_lik[N];
int y_hat_mat[S, T]; // ppcheck for each S*T combination
real y_hat_time[S]; // predicted failure time for each sample
int y_hat_event[S]; // predicted event (0:censor, 1:event)
// log-likelihood, for loo
for (n in 1:N) {
log_lik[n] = poisson_log_lpmf(event[n] | log_hazard[n]);
}
// posterior predicted values
for (samp in 1:S) {
int sample_alive;
sample_alive = 1;
for (tp in 1:T) {
if (sample_alive == 1) {
real log_haz;
int n;
int pred_y;
// determine predicted value of y
n = n_trans[samp, tp];
log_haz = x[n,]*beta + log_baseline[tp];
if (log_haz < log(pow(2, 30)))
pred_y = poisson_log_rng(log_haz);
else
pred_y = 9;
// mark this patient as ineligible for future tps
// note: deliberately make 9s ineligible
if (pred_y >= 1) {
sample_alive = 0;
y_hat_time[samp] = t_obs[tp];
y_hat_event[samp] = 1;
}
// save predicted value of y to matrix
y_hat_mat[samp, tp] = pred_y;
}
else if (sample_alive == 0) {
y_hat_mat[samp, tp] = 9;
}
} // end per-timepoint loop
// if patient still alive at max
//
if (sample_alive == 1) {
y_hat_time[samp] = t_obs[T];
y_hat_event[samp] = 0;
}
} // end per-sample loop
}
In [3]:
d = stancache.cached(
survivalstan.sim.sim_data_exp_correlated,
N=100,
censor_time=20,
rate_form='1 + sex',
rate_coefs=[-3, 0.5],
)
d['age_centered'] = d['age'] - d['age'].mean()
d.head()
INFO:stancache.stancache:sim_data_exp_correlated: cache_filename set to sim_data_exp_correlated.cached.N_100.censor_time_20.rate_coefs_54462717316.rate_form_1 + sex.pkl
INFO:stancache.stancache:sim_data_exp_correlated: Loading result from cache
Out[3]:
| age | sex | rate | true_t | t | event | index | age_centered | |
|---|---|---|---|---|---|---|---|---|
| 0 | 59 | male | 0.082085 | 20.948771 | 20.000000 | False | 0 | 4.18 |
| 1 | 58 | male | 0.082085 | 12.827519 | 12.827519 | True | 1 | 3.18 |
| 2 | 61 | female | 0.049787 | 27.018886 | 20.000000 | False | 2 | 6.18 |
| 3 | 57 | female | 0.049787 | 62.220296 | 20.000000 | False | 3 | 2.18 |
| 4 | 55 | male | 0.082085 | 10.462045 | 10.462045 | True | 4 | 0.18 |
In [4]:
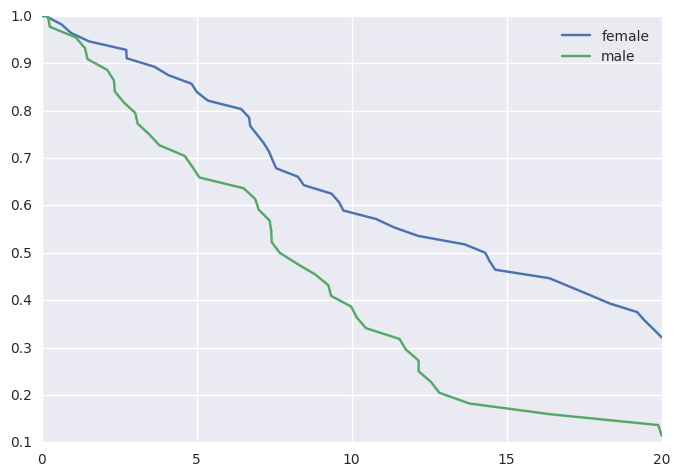
survivalstan.utils.plot_observed_survival(df=d[d['sex']=='female'], event_col='event', time_col='t', label='female')
survivalstan.utils.plot_observed_survival(df=d[d['sex']=='male'], event_col='event', time_col='t', label='male')
plt.legend()
Out[4]:
<matplotlib.legend.Legend at 0x7f9fac008eb8>
In [5]:
dlong = stancache.cached(
survivalstan.prep_data_long_surv,
df=d, event_col='event', time_col='t'
)
INFO:stancache.stancache:prep_data_long_surv: cache_filename set to prep_data_long_surv.cached.df_33772694934.event_col_event.time_col_t.pkl
INFO:stancache.stancache:prep_data_long_surv: Loading result from cache
In [6]:
dlong.head()
Out[6]:
| age | sex | rate | true_t | t | event | index | age_centered | key | end_time | end_failure | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 59 | male | 0.082085 | 20.948771 | 20.0 | False | 0 | 4.18 | 1 | 20.000000 | False |
| 1 | 59 | male | 0.082085 | 20.948771 | 20.0 | False | 0 | 4.18 | 1 | 12.827519 | False |
| 2 | 59 | male | 0.082085 | 20.948771 | 20.0 | False | 0 | 4.18 | 1 | 10.462045 | False |
| 3 | 59 | male | 0.082085 | 20.948771 | 20.0 | False | 0 | 4.18 | 1 | 0.196923 | False |
| 4 | 59 | male | 0.082085 | 20.948771 | 20.0 | False | 0 | 4.18 | 1 | 9.244121 | False |
In [7]:
testfit = survivalstan.fit_stan_survival_model(
model_cohort = 'test model',
model_code = survivalstan.models.pem_survival_model_gamma,
df = dlong,
sample_col = 'index',
timepoint_end_col = 'end_time',
event_col = 'end_failure',
formula = '~ age_centered + sex',
iter = 5000,
chains = 4,
seed = 9001,
FIT_FUN = stancache.cached_stan_fit,
)
INFO:stancache.stancache:Step 1: Get compiled model code, possibly from cache
INFO:stancache.stancache:StanModel: cache_filename set to anon_model.cython_0_25_1.model_code_72990130769.pystan_2_12_0_0.stanmodel.pkl
INFO:stancache.stancache:StanModel: Loading result from cache
INFO:stancache.stancache:Step 2: Get posterior draws from model, possibly from cache
INFO:stancache.stancache:sampling: cache_filename set to anon_model.cython_0_25_1.model_code_72990130769.pystan_2_12_0_0.stanfit.chains_4.data_64545635565.iter_5000.seed_9001.pkl
INFO:stancache.stancache:sampling: Starting execution
INFO:stancache.stancache:sampling: Execution completed (0:02:26.153391 elapsed)
INFO:stancache.stancache:sampling: Saving results to cache
/home/jacquelineburos/miniconda3/envs/python3/lib/python3.5/site-packages/stancache/stancache.py:251: UserWarning: Pickling fit objects is an experimental feature!
The relevant StanModel instance must be pickled along with this fit object.
When unpickling the StanModel must be unpickled first.
pickle.dump(res, open(cache_filepath, 'wb'), pickle.HIGHEST_PROTOCOL)
/home/jacquelineburos/miniconda3/envs/python3/lib/python3.5/site-packages/stanity/psis.py:228: FutureWarning: elementwise comparison failed; returning scalar instead, but in the future will perform elementwise comparison
elif sort == 'in-place':
/home/jacquelineburos/miniconda3/envs/python3/lib/python3.5/site-packages/stanity/psis.py:246: VisibleDeprecationWarning: using a non-integer number instead of an integer will result in an error in the future
bs /= 3 * x[sort[np.floor(n/4 + 0.5) - 1]]
/home/jacquelineburos/miniconda3/envs/python3/lib/python3.5/site-packages/stanity/psis.py:262: RuntimeWarning: overflow encountered in exp
np.exp(temp, out=temp)
/home/jacquelineburos/miniconda3/envs/python3/lib/python3.5/site-packages/stanity/psis.py:246: RuntimeWarning: divide by zero encountered in true_divide
bs /= 3 * x[sort[np.floor(n/4 + 0.5) - 1]]
/home/jacquelineburos/miniconda3/envs/python3/lib/python3.5/site-packages/stanity/psis.py:250: RuntimeWarning: invalid value encountered in multiply
temp = ks[:,None] * x
/home/jacquelineburos/miniconda3/envs/python3/lib/python3.5/site-packages/stanity/psis.py:267: RuntimeWarning: invalid value encountered in greater_equal
dii = w >= 10 * np.finfo(float).eps
/home/jacquelineburos/miniconda3/envs/python3/lib/python3.5/site-packages/stanity/psis.py:282: RuntimeWarning: invalid value encountered in double_scalars
sigma = -k / b
In [8]:
survivalstan.utils.print_stan_summary([testfit], pars='lp__')
mean se_mean sd 2.5% 50% 97.5% Rhat
lp__ -1034.96497 0.18312 7.354494 -1050.563484 -1034.543604 -1021.53023 1.000819
In [9]:
survivalstan.utils.print_stan_summary([testfit], pars='log_baseline')
mean se_mean sd 2.5% 50% 97.5% Rhat
log_baseline[0] -5.540533 0.026349 1.317162 -8.741271 -5.317482 -3.605955 1.000660
log_baseline[1] -5.540373 0.026410 1.312295 -8.765512 -5.305697 -3.661229 1.000160
log_baseline[2] -5.533987 0.025182 1.277367 -8.563403 -5.341926 -3.613802 1.000899
log_baseline[3] -5.499061 0.023197 1.266738 -8.526801 -5.300919 -3.598318 1.000996
log_baseline[4] -5.529027 0.029142 1.376488 -8.883094 -5.280803 -3.553426 1.001002
log_baseline[5] -5.471047 0.025521 1.260655 -8.429872 -5.272214 -3.596805 1.002028
log_baseline[6] -5.499416 0.034998 1.321609 -8.548750 -5.291451 -3.584369 1.003210
log_baseline[7] -5.464198 0.024734 1.288292 -8.466082 -5.228081 -3.575405 1.000619
log_baseline[8] -5.466310 0.027385 1.284197 -8.583571 -5.262634 -3.536853 1.001117
log_baseline[9] -5.416356 0.024357 1.279819 -8.469762 -5.221550 -3.528211 1.001357
log_baseline[10] -5.440701 0.027773 1.306535 -8.676018 -5.228972 -3.541475 1.001608
log_baseline[11] -5.434051 0.027698 1.305317 -8.664646 -5.225114 -3.512998 0.999949
log_baseline[12] -5.370823 0.028533 1.284318 -8.459077 -5.161179 -3.454565 1.001136
log_baseline[13] -5.393917 0.024404 1.280480 -8.626593 -5.192589 -3.486274 1.000423
log_baseline[14] -5.364330 0.025443 1.273700 -8.327442 -5.166064 -3.490194 1.002779
log_baseline[15] -5.357747 0.025662 1.282847 -8.510490 -5.145634 -3.463617 1.002548
log_baseline[16] -5.378575 0.027974 1.302219 -8.521636 -5.152384 -3.489239 1.003528
log_baseline[17] -5.295181 0.026170 1.249062 -8.246395 -5.115480 -3.442103 1.004022
log_baseline[18] -5.346658 0.027128 1.301594 -8.462238 -5.129009 -3.403453 1.002558
log_baseline[19] -5.293308 0.027616 1.280204 -8.270132 -5.103891 -3.405552 1.000711
log_baseline[20] -5.312085 0.024626 1.318119 -8.478142 -5.086743 -3.394770 1.000745
log_baseline[21] -5.277845 0.026557 1.264723 -8.303782 -5.068627 -3.349496 1.000715
log_baseline[22] -5.306103 0.027747 1.309989 -8.480791 -5.098819 -3.372876 1.002474
log_baseline[23] -5.240126 0.024418 1.274211 -8.374662 -5.031179 -3.368183 1.002631
log_baseline[24] -5.180366 0.023456 1.229393 -8.199401 -4.991827 -3.339248 1.002037
log_baseline[25] -5.220781 0.025189 1.279213 -8.155421 -5.026628 -3.347359 0.999862
log_baseline[26] -5.198388 0.027133 1.293306 -8.334439 -4.988685 -3.310959 1.002848
log_baseline[27] -5.145882 0.024486 1.269478 -8.201074 -4.960108 -3.261169 1.000358
log_baseline[28] -5.112184 0.023308 1.235079 -8.159944 -4.913842 -3.245869 1.001038
log_baseline[29] -5.130311 0.028653 1.303939 -8.381742 -4.914959 -3.271805 1.001287
log_baseline[30] -5.197454 0.026676 1.342558 -8.362530 -4.956216 -3.213312 1.000961
log_baseline[31] -5.188365 0.027795 1.344816 -8.474813 -4.969168 -3.277665 1.002005
log_baseline[32] -5.102617 0.024780 1.260118 -8.178528 -4.901117 -3.213594 1.000780
log_baseline[33] -5.075221 0.024387 1.227845 -7.991722 -4.885576 -3.214388 1.000436
log_baseline[34] -5.110409 0.029528 1.336298 -8.447845 -4.872393 -3.193095 1.001111
log_baseline[35] -5.031990 0.024814 1.248103 -8.051273 -4.841412 -3.165030 1.000698
log_baseline[36] -5.050843 0.025298 1.288200 -8.189802 -4.835042 -3.140867 1.002413
log_baseline[37] -5.027862 0.025181 1.274591 -7.993631 -4.829429 -3.130617 1.002734
log_baseline[38] -5.043253 0.031843 1.332076 -8.392334 -4.800582 -3.117772 1.001792
log_baseline[39] -5.009148 0.027024 1.286125 -8.114673 -4.801411 -3.083061 1.001948
log_baseline[40] -4.977261 0.022727 1.253310 -8.021432 -4.786938 -3.099191 1.000618
log_baseline[41] -4.973488 0.026404 1.297564 -8.165326 -4.762586 -3.063354 1.000620
log_baseline[42] -4.976570 0.026160 1.289808 -8.134780 -4.785349 -3.061472 1.000685
log_baseline[43] -4.919019 0.025599 1.277389 -8.050034 -4.700221 -3.016657 1.001715
log_baseline[44] -4.900334 0.025927 1.293227 -8.049396 -4.679596 -2.980225 1.000656
log_baseline[45] -4.907134 0.025745 1.276647 -8.046290 -4.690973 -3.021486 1.001499
log_baseline[46] -4.855415 0.023345 1.255215 -7.826891 -4.654950 -2.972896 1.001151
log_baseline[47] -4.832234 0.021958 1.254851 -7.809152 -4.639160 -2.926565 1.001058
log_baseline[48] -4.798222 0.024395 1.255120 -7.870438 -4.580276 -2.924569 1.000580
log_baseline[49] -4.838834 0.029046 1.346472 -8.135627 -4.612250 -2.866454 1.001520
log_baseline[50] -4.760367 0.024182 1.265330 -7.845615 -4.552539 -2.875869 1.000354
log_baseline[51] -4.737922 0.024380 1.249825 -7.791359 -4.524863 -2.860117 1.000065
log_baseline[52] -4.751358 0.028862 1.327670 -8.044268 -4.540209 -2.862803 1.000918
log_baseline[53] -4.685420 0.023722 1.284065 -7.852333 -4.469523 -2.795754 1.001032
log_baseline[54] -4.695464 0.025316 1.294588 -7.810316 -4.503222 -2.782197 1.000505
log_baseline[55] -4.662545 0.027774 1.317164 -7.848580 -4.440736 -2.771303 1.000641
log_baseline[56] -4.669330 0.030262 1.321870 -7.914412 -4.434960 -2.743924 1.000618
log_baseline[57] -4.620962 0.025575 1.282324 -7.585949 -4.400851 -2.737336 1.003473
log_baseline[58] -4.564812 0.025214 1.287904 -7.671804 -4.338766 -2.704413 1.001306
log_baseline[59] -4.562128 0.030414 1.350609 -7.910983 -4.324704 -2.648129 1.000886
log_baseline[60] -4.542367 0.032122 1.338757 -7.768437 -4.320009 -2.624694 1.002409
log_baseline[61] -4.480764 0.025349 1.287803 -7.550987 -4.280852 -2.593134 1.001754
log_baseline[62] -4.430831 0.024307 1.228657 -7.382741 -4.239083 -2.589439 1.001206
log_baseline[63] -4.395725 0.023673 1.273268 -7.384986 -4.209973 -2.479231 1.000442
log_baseline[64] -4.346682 0.025621 1.266635 -7.426116 -4.141308 -2.442702 1.002046
log_baseline[65] -4.312951 0.024879 1.298957 -7.481565 -4.094432 -2.411871 1.001782
log_baseline[66] -4.272058 0.023535 1.271993 -7.300271 -4.066569 -2.414926 1.001380
log_baseline[67] -4.278248 0.024941 1.301696 -7.406780 -4.063855 -2.381025 1.001246
log_baseline[68] -4.239232 0.022731 1.255980 -7.282352 -4.042431 -2.363243 1.000641
log_baseline[69] -4.220383 0.023864 1.257355 -7.227408 -4.033891 -2.300163 1.000607
log_baseline[70] -4.174461 0.033438 1.387179 -7.389505 -3.925402 -2.265936 1.002038
log_baseline[71] -4.090127 0.022568 1.252697 -7.085192 -3.892866 -2.207512 1.002348
log_baseline[72] -4.110447 0.027878 1.315899 -7.399702 -3.860361 -2.205056 1.001732
log_baseline[73] -4.056023 0.027877 1.311094 -7.247058 -3.837001 -2.137026 1.001115
log_baseline[74] -4.023769 0.024615 1.255600 -7.067530 -3.820071 -2.142365 1.001948
log_baseline[75] -4.049963 0.026498 1.295967 -7.201009 -3.854413 -2.140042 1.000684
log_baseline[76] -4.047071 0.028314 1.357597 -7.297987 -3.803428 -2.082792 1.001065
log_baseline[77] -322.669893 5.131864 200.339993 -685.976286 -304.462026 -18.223910 1.002720
In [10]:
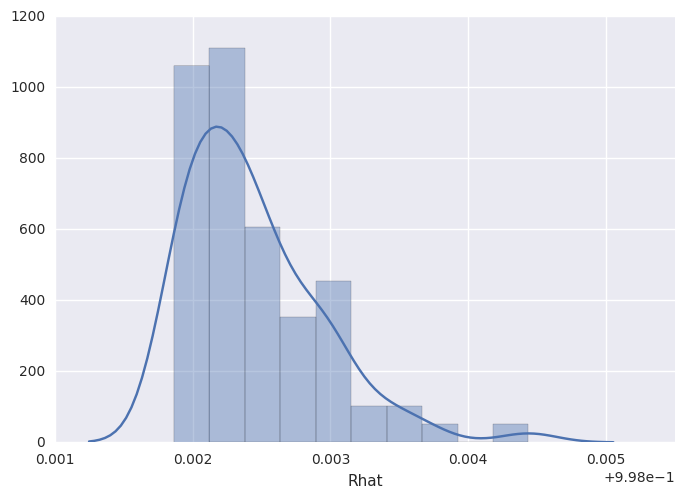
survivalstan.utils.plot_stan_summary([testfit], pars='baseline')
INFO:survivalstan.utils:Warning - 1 rows removed due to NaN values for Rhat. This may indicate a problem in your model estimation.
In [11]:
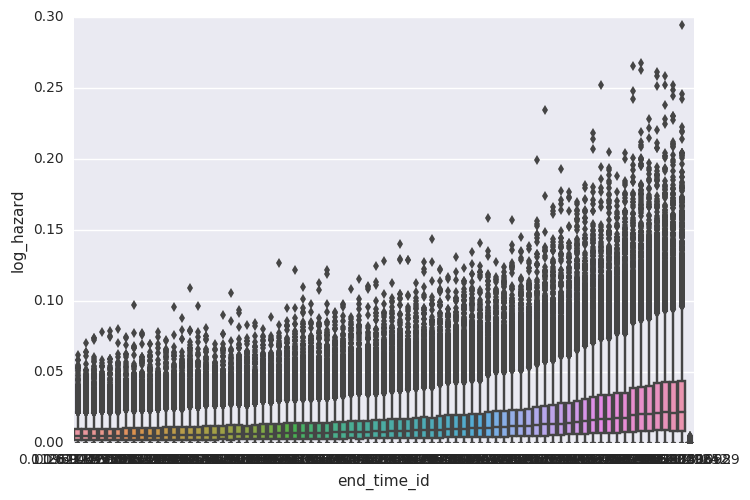
survivalstan.utils.plot_coefs([testfit], element='baseline')
In [12]:
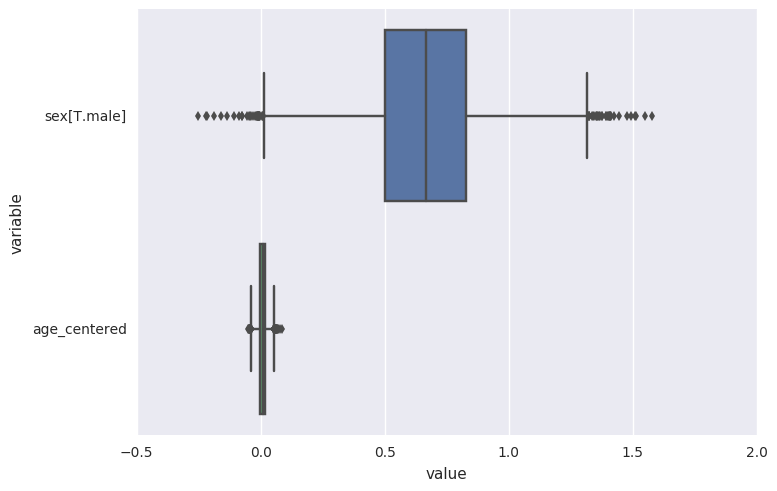
survivalstan.utils.plot_coefs([testfit])
In [13]:
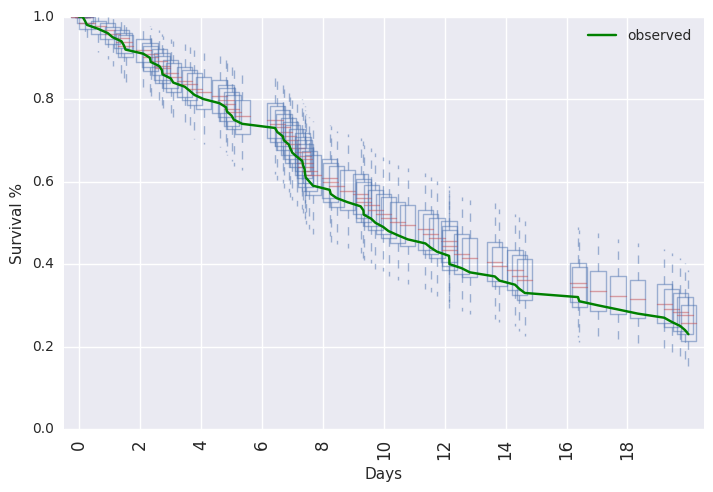
survivalstan.utils.plot_pp_survival([testfit], fill=False)
survivalstan.utils.plot_observed_survival(df=d, event_col='event', time_col='t', color='green', label='observed')
plt.legend()
Out[13]:
<matplotlib.legend.Legend at 0x7f9ec3bcba20>
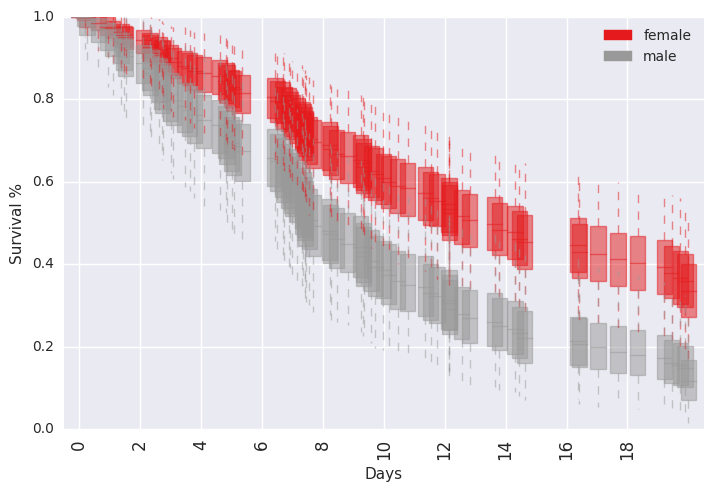
In [14]:
survivalstan.utils.plot_pp_survival([testfit], by='sex')
In [15]:
ppsurv = survivalstan.utils.prep_pp_survival_data([testfit], by='sex')
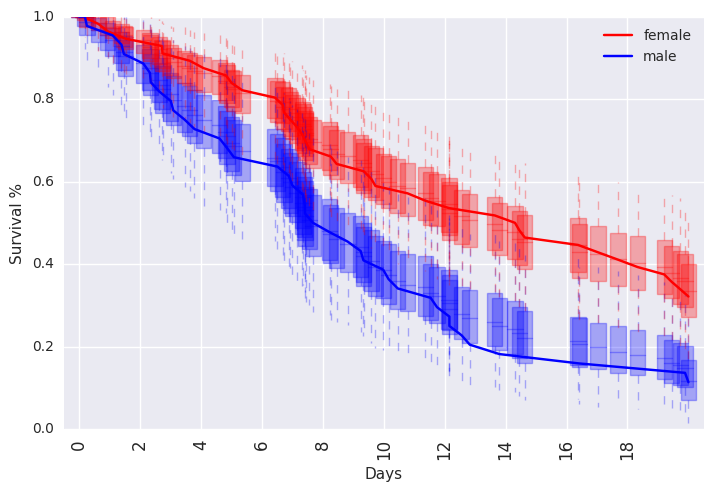
In [16]:
subplot = plt.subplots(1, 1)
survivalstan.utils._plot_pp_survival_data(ppsurv.query('sex == "male"').copy(),
subplot=subplot, color='blue', alpha=0.3)
survivalstan.utils._plot_pp_survival_data(ppsurv.query('sex == "female"').copy(),
subplot=subplot, color='red', alpha=0.3)
survivalstan.utils.plot_observed_survival(df=d[d['sex']=='female'], event_col='event', time_col='t',
color='red', label='female')
survivalstan.utils.plot_observed_survival(df=d[d['sex']=='male'], event_col='event', time_col='t',
color='blue', label='male')
plt.legend()
Out[16]:
<matplotlib.legend.Legend at 0x7f9f9714d7f0>
In [17]: